Write-Up #4--Euler's Line
The use of technology in geometry classes allows teacher's to investigate
more ideas in various subjects. If teacher must wait on the students to
complete constructions during class time or even at home, there is a lot
of time that is wasted. The students will also get extremely tired of doing
many constructions demonstrating the same concept for the three types of
triangles (acute, obtuse, and right). Therefore, the use of any geometry
software package in a class will decrease the time spent on the "grunt
work" and leave more time for the "ah-ha" feeling that students
get when they discover an idea by using the software.
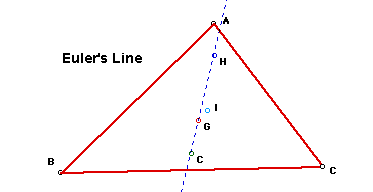
One example of such an idea is in the discover of Euler's Line of a Triangle.
Euler discovered that the centroid, the orthocenter, and the circumcenter
of a triangle lie on the same line. This line is now named for him. By using
a geometry package, (Geometer's Sketchpad, in this case) the students can
find the centers of the triangle and explore their movement as the shape
of the triangle changes.
Click on the triangle to see an animation of the triangle on Geometer's
Sketchpad.
Once the students create the triangle with the centers, they can manipulate
the triangle to see what happens with the different types of triangles.
They can also see what happens in very special cases, like a right triangle.
Directions for creating Euler's Line:
1. Create any triangle.
2. Construct the centroid (G) of the triangle. A centroid is the intersection
of the medians of the
triangle. A median is the segment from a vertex to the midpoint of the opposite
side.
3. Construct the orthocenter (H) of the triangle. The orthocenter is the
intersection of the altitudes of the triangle. An altitudes is the perpendicular
segment from a vertex to the opposite side.
4. Construct the circumcenter (C) of the triangle. The circumcenter is equidistant
from the three vertices of the triangle. It lies on the perpendicular bisector.
5. Construct the incenter (I) of the triangle. The incenter lies on the
intersection of the angle bisectors of the vertices.
6. Draw a line from the orthocenter to the circumcenter.
If you are interested in the Geometer's Sketchpad script, click
here.
First, try some manipulations yourself. Would you like to see some examples
with specific triangles: acute triangles,
obtuse triangles, and right
triangles?
Return to Write-Ups for EMT 668 Page
Return to Dawn's Home Page

